O Que Mais Cai na Prova de Matemática do Enem

A prova de Matemática do Enem é certamente a que mais apavora a galera, que sonha com uma vaga na Universidade. Saber O que mais cai na prova de Matemática do Enem é de suma importância para melhorar significativamente a sua preparação.
Se o seu objetivo é passar no Enem, não basta estar preparado, é preciso conhecer o estilo da prova e dar mais ênfase aos conteúdos mais cobrados.
Matemática é considerada a prova mais importante por ser a única prova com 45 questões, além de pertencer a uma única área do conhecimento. Essa prova exigirá do aluno um bom domínio de conceitos matemáticos e da Matemática básica do ensino fundamental. As questões apresentam enunciados repletos de informações, além de conter muitos gráficos para interpretar.
O que mais cai na prova de Matemática do Enem
Temos quase 30 assuntos importantes que fazem parte do Ensino médio. Falaremos aqui de apenas 5 assuntos que representarão mais de 80 % desta prova, considerando todas as edições do Enem desde 2009
1. Geometria (27,2%)
Cuidado, pois aqui temos 3 Geometrias: Geometria Plana, espacial e a Geometria Analítica.
Na Geometria Plana Espacial temos os famosos cálculos de áreas (contidos no plano) e volumes (contidos no espaço) de figuras conhecidas por todos.
Vídeo aulas de Geometria Plana
Vídeo Aulas de Geometria Espacial
Vídeo Aulas de Geometria Analítica
Exemplo (O que mais cai na prova de Matemática do Enem)
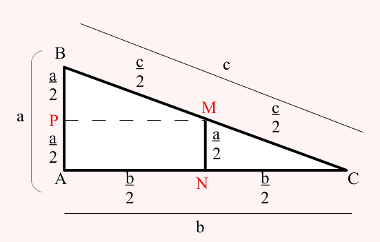
(ENEM) Em canteiros de obras de construção civil, é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde
a) à mesma área do triângulo AMC.
b) à mesma área do triângulo BNC.
c) à metade da área formada pelo triângulo ABC.
d) ao dobro da área do triângulo MNC.
e) ao triplo da área do triângulo MNC.
Para solucionar essa questão, devemos determinar a medida dos segmentos BP, PA, BM, MC, AN e NC. Essas medidas são estabelecidas por meio do ponto médio, que é o ponto que divide o segmento em duas partes iguais. Observe no desenho as medidas dos segmentos de acordo com os seus três pontos médios: M, N e P.
Agora que sabemos as medidas dos segmentos descritos anteriormente, podemos calcular a área.
Dados para o cálculo da área do triângulo MCN:
base = a/2 e altura = b/2
Fórmula para calcular a área do triângulo: A = (Base x Altura)/2
Cálculo da área do triângulo MCN:
AMCN = (a/2 . b/2)/2
AMCN = ab/8
8 . AMCN = ab
Dados para o cálculo da área do triângulo BAC: a = base b = altura
Fórmula para calcular a área do triângulo: A = (Base x Altura)/2
Cálculo da área do triângulo MCN:
ABAC =a.b/2
ABAC = 8 . AMCN/2
ABAC = 4 AMCN
ABAC = 3 AMCN + AMCN
Logo, AABMN = 3 AMCN
A área a ser calçada corresponde a 3 AMCN . Letra “e”.
O que mais cai na prova de Matemática do Enem
2. Gráficos (22,8%)
Saber interpretar os diferentes tipos de gráficos será fundamental para obter uma boa nota no Enem.
São eles: de pizza, da barras, de linhas e de colunas
Exemplo (O que mais cai na prova de Matemática do Enem)
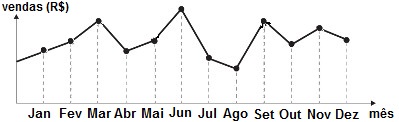
(ENEM) O dono de uma farmácia resolveu colocar à vista do público o gráfico mostrado a seguir, que apresenta a evolução do total de vendas (em Reais) de certo medicamento ao longo do ano de 2011.
Questão com interpretação de gráficos no Enem de 2012
De acordo com o gráfico, os meses em que ocorreram, respectivamente, a maior e a menor venda absolutas em 2011 foram:
a) março e abril.
b) março e agosto.
c) agosto e setembro.
d) junho e setembro.
e) junho e agosto.
Para resolver essa questão, basta analisar o gráfico dado no exercício. Para cada mês há um ponto que corresponde ao valor das vendas desse mês. Mesmo que não tenhamos valores numéricos para cada mês, podemos perceber que, quanto mais alto o ponto, maior a venda, e quanto mais baixo o ponto, menor a venda desse mês. Facilmente observamos que o mais alto dos pontos corresponde ao mês de Junho, e o mais baixo dos pontos corresponde ao mês de Agosto. Podemos concluir com essa análise que o mês de junho teve a maior venda absoluta, e o mês de Agosto teve a menor venda absoluta. Portanto, a alternativa correta é a letra e.
O que mais cai na prova de Matemática do Enem

Matemática para Enem + (Química, Física, Biologia, Português, Redação, Filosofia, Sociologia e muito mais!
3. Razão, Proporção e Escala (13,3%)
Na matemática, a palavra razão significa divisão, proporção é a igualdade entre duas razões e escala é a aplicação da razão entre duas grandezas.
Um exemplo clássico seria aquela questão de uma área (real) representada em um mapa (desenho) ou folha de papel. o comprimento de um desenho e o seu tamanho real. Nesse caso essas medidas de escala também são diretamente proporcionais às medidas em tamanho real.
Exemplo (O que mais cai na prova de Matemática do Enem)
(ENEM) A Figura 1 representa uma gravura retangular com 8 m de comprimento e 6 m de altura.
Deseja-se reproduzi-la numa folha de papel retangular com 42 cm de comprimento e 30 cm de altura, deixando livres 3 cm em cada margem, conforme a Figura 2
A reprodução da gravura deve ocupar o máximo possível da região disponível, mantendo-se as proporções da Figura 1. PRADO, A. C. Superinteressante, ed. 301, fev. 2012 (adaptado).
A escala da gravura reproduzida na folha de papel é
a) 1 : 3
b) 1 : 4
c) 1 : 20
d) 1 : 25
e) 1 : 32
Para resolver essa questão, devemos primeiramente descrever os dados:
Dados:
→ Figura retangular 1:
⇒ Comprimento = 8 m
⇒ Altura = 6 m
→ Figura retangular 2:
⇒ Comprimento = 42 cm → 42 cm – 6 cm = 36 cm → (Subtraímos 6 de 42 porque temos que retirar o valor referente às margens da folha de papel retangular.)
⇒ Altura = 30 cm → 30 cm – 6 cm = 24 cm → ( Subtraímos 6 de 30 porque temos que retirar o valor referente às margens da folha de papel retangular.)
Solução da questão:
As unidades de medida da figura retangular 1 em relação à figura retangular 2 são diferentes. Devemos colocar todas as medidas da questão na mesma unidade. Vamos transformá-las de metro para centímetro.
Figura retangular 1: Comprimento = 8m → 8 x 100 = 800 cm
Altura = 6 m → 6 x 100 = 600 cm
Agora que todas as medidas estão em centímetros, podemos estruturar as razões. Lembre-se de que a razão é formada por elementos que possuem a mesma atribuição. Nessa questão, relacionaremos comprimento com comprimento e altura com altura.
800 = 22,2 = 22
36
600 = 25
24
Nessa questão, precisamos obter a escala máxima para a gravura. Sendo assim, seu valor será 1/25 Isso porque 25 é maior que 22. A alternativa correta é a letra “d”.
O que mais cai na prova de Matemática do Enem
4. Funções (9,2%):
Aqui temos questões que envolverão principalmente as funções de primeiro e segundo graus.
Exemplo (O que mais cai na prova de Matemática do Enem)
(ENEM)O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ 100 000,00 por km construído (n), acrescidos de um valor fixo de R$ 350 000,00, enquanto a segunda cobrou R$ 120 000,00 por km construído (n), acrescidos de um valor fixo de R$ 150 000,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada.
Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?
a) 100n + 350 = 120n + 150 ←
b) 100n + 150 = 120n + 350
c) 100(n + 350) = 120(n + 150)
d) 100(n + 350 000) = 120(n + 150 000)
e) 350(n + 100 000) = 150(n + 120 000)
Resolução:
Vamos identificar a primeira empresa descrita como Empresa A e a segunda como Empresa B. Podemos utilizar funções do 1° grau para descrever o preço cobrado por cada empresa. A empresa A tem um custo fixo de R$ 350 000,00 e cobra R$ 100 000,00 por km construído (n), então 350 000 é o termo constante e 100 000 é o coeficiente da variável n. A função que representa a empresa A é:
yA = an + b
yA = 100000.n + 350000
Para a empresa B, podemos afirmar que o custo fixo de R$ 150 000,00 é o termo constante e o valor de R$ 120 000,00 por km construído (n) é o coeficiente da variável n. Portanto, a função do preço cobrado pela empresa B é:
yB = an + b
yB = 120000.n + 150000
O valor cobrado pelas duas empresas será o mesmo quando yA = yB, então, temos:
yA = yB
100000.n + 350000 = 120000.n + 150000
Dividindo ambos os membros da equação por 1000, teremos:
100.n + 350 = 120.n + 150
A alternativa que apresenta a equação correta é a letra a.
As funções de primeiro e segundo graus costumam ser as mais recorrentes na prova. Com menos intensidade, também aparecem as funções trigonométricas, exponenciais e logarítmicas.
O que mais cai na prova de Matemática do Enem
5. Porcentagem (10,1%):
Veja como calcular Porcentagem rapidamente:
A porcentagem é uma razão que tem o denominador igual a 100. Ou seja, um número x%.
Porcentagem significa “por cento” e é representada pelo símbolo de porcentagem “%”. Além da representação pelo símbolo, também é possível representar uma porcentagem por um número decimal ou por uma razão. Aprenda mais sobre Porcentagem.
Exemplo (O que mais cai na prova de Matemática do Enem)
(ENEM) Uma enquete, realizada em março de 2010, perguntava aos internautas se eles acreditavam que as atividades humanas provocam o aquecimento global. Eram três as alternativas possíveis e 279 internautas responderam à enquete, como mostra o gráfico:
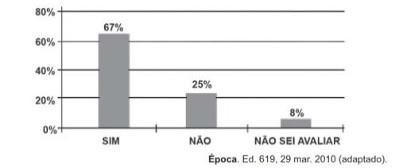
Questão do Enem de 2011 que envolve o cálculo da porcentagem de um número
Analisando os dados do gráfico, quantos internautas responderam “NÃO” à enquete:
a) Menos de 23.
b) Mais de 23 e menos de 25.
c) Mais de 50 e menos de 75.
d) Mais de 100 e menos de 190.
e) Mais de 200.
Se houve a participação de 279 internautas e apenas 25% destes responderam “não”, basta nós utilizarmos o cálculo da porcentagem de um número para descobrirmos quanto é 25% de 279. Teremos:
25% de 279 = (25/100) . 279 = 69,75
Então, 25% de 279 internautas equivale a 69,75 pessoas. A alternativa correta é a letra c, que nos diz que a quantidade de internautas que responderam “não” é mais de 50 e menos de 75 pessoas.